Xin phép được đăng lại bài của cô Thái Trà My để mọi người tham khảo ak!
Submodular function được định nghĩa như sau:
Định nghĩa 1: Cho một set function

trên mọi tập con của tập
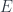
. Hàm

được gọi là submodular function khi với bất kỳ hai tập con

, ta có:
Ví dụ:
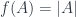
là một submodular function.
Định nghĩa trên còn tương đương với định lý sau:
Định lý 1: Xét một set function

. Nếu

là submodular function thì với mọi

và

, ta có:
Định lý 1 ngụ ý rằng thêm một phần tử vào tập

sẽ có lợi hơn thêm nó vào mộ tập lớn hơn

. Nghĩa là, càng sớm càng tốt.
Tại sao chúng ta lại quan tâm đến submodular function? Bởi chúng đóng một vai trò rất quan trọng trong toán tối ưu và thuật toán xấp xỉ (approximation algorithms)
Có rất nhiều phương pháp trong thuật toán xấp xỉ, từ thuật toán tổ hợp (combinatorics) tới quy hoạch tuyến tính (linear programming) và semi-definite programming. Trong đó, thuật toán tham lam (greedy algorithms) là một trong những thuật toán phổ biến nhất và tính ứng dụng rất cao bởi độ đơn giản của nó cùng với độ phức tạp thấp về thời gian.
Tuy nhiên, phân tích tỉ lệ xấp xỉ (approximation ratio) của thuật toán tham lam vô cùng tricky và thú vị. Nếu hàm tham lam (greedy function) của một thuật toán tham lam là submodular function thì việc phân tích tỉ lệ xấp xỉ trở nên đơn giản hơn nhiều. Chúng ta hãy xét một vài ví dụ sau đây.
Set Cover: Cho trước một tập vũ trụ

có

phần tử và một họ
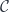
tập con của

. Tìm họ con nhỏ nhất

phủ tất cả các phần tử của

.
Define

(i.e. tổng số phần tử trong

). Xét thuật toán tham lam sau:
Algorithm 1:
while

do
return

Trong Algorithm 1, cho mỗi iteration, chúng ta chọn một tập con sao cho phủ được nhiều phần tử chưa được phủ tại thời điểm đó. Chúng ta sẽ chứng minh rằng Algorithm 1 có tỉ lệ xấp xỉ là
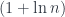
với
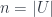
. (Chú ý rằng với bài toán minimization, thì tỉ lệ xấp xỉ
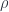
được định nghĩa như sau:

trong đó

là giá trị tối ưu và

là giá trị lời giải.)
Trước tiên, chúng ta chứng minh hai bổ đề sau:
Bổ đề 1: Hàm

là submodular function
và monotone increasing.
Chứng minh: Bài tâp.
Bổ đề 2: Giả sử
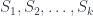
được chọn bởi Algorithm 1. Ký hiệu

và

là giá trị tối ưu (optimal value), ta có:
Chứng minh: Ký hiệu

. Gọi

là lời giải tối ưu (optimal solution). Và ký hiệu

. Tại mỗi iteration

, theo Algorithm 1, ta có:
Suy ra,

(theo Bổ đề 1)
Do đó, ta có:
Từ bổ đề 2, chúng ta dễ dàng chứng minh Định lý sau:
Định lý 2: Algorithm 1 có tỉ lệ xấp xỉ là
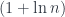
Chứng minh: Theo Bổ đề 2, ta có:
Chọn

là số nguyên dương lớn nhất thỏa mãn:

. Ta có:
Do đó,
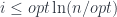
. Suy ra

Bây giờ, giả sử mỗi tập con của

có một khối lượng và ta muốn tìm họ con với khối lượng nhỏ nhất. Ta cần phải làm gì?
Weighted Set Cover: Cho trước một tập vũ trụ

có

phần tử , một họ
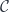
tập con của

với weight function

. Tìm họ con có khối lượng nhỏ nhất

phủ tất cả các phần tử của

.
Sử dụng hàm

ở trên, thay đổi Algorithm 1 một tí, ta có:
Algorithm 2:
while

do
return

Định lý 3: Algorithm 2 có tỉ lệ xấp xỉ là
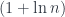
Chứng minh: Bài tập.
Tổng quát hóa, ta có:
Bài toán tổng quát : Xét một hàm monotone increasing và submodular function

trên tất cả tập con của tập
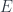
và một cost function

. Định nghĩa
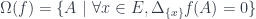
. Xét bài toán sau:
minimize
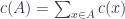
sao cho
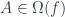
Lời giải: Để giải bài toán tổng quát trên, ta có thuật toán tham lam như sau:
Algorithm 3:
while tồn tại
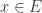
sao cho
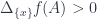
do
return

Định lý 4: Nếu

,

là hàm số dương (integer function), monotone increasing, submodular function, và
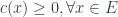
, Algorithm 3 sẽ có tỉ lệ xấp xỉ là
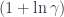
với
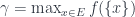
.
Chứng minh: Giả sử

là các phần tử được Algorithm 3 chọn theo thứ tự như vậy. Ký
hiệu
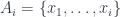
và

.
Gọi

là lời giải tối ưu. Với mỗi

, đặt
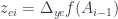
. Cho đơn giản, ký hiệu
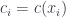
và
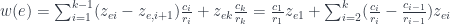
Trước tiên, ta chứng minh hai mệnh đề sau:
Mệnh đề 1: 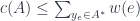
Để chứng minh Mệnh đề 1, ta có:
Hơn nữa, hàm

là submodular và monotone increasing, ta có:
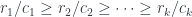
Vì vậy, để chứng minh Mệnh đề 1, chúng ta chỉ cần chứng minh
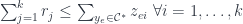
là xong.
Ta có,
Vậy là chúng ta đã chứng minh xong Mệnh đề 1.
Mệnh đề 2: 
, ta có:

Chứng minh Mệnh đề 2 khá đơn giản. Chú ý rằng
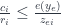
(theo Algorithm 3} và
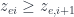
(

là monotone increasing và submodular)
Vì vậy, chúng ta dễ dàng có:
Có được bước cuối cùng vì
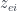
là số nguyên. Chú ý rằng

. Nên từ hai mệnh đề, ta chứng minh xong định lý 4.
Ghi chú: Nếu

, chúng ta đặt
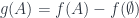
. Lúc đó,

là hàm nguyên, monotone increasing, submodular, và
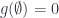
. Suy ra,
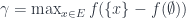
.
Vậy cho mỗi bài minimization, nếu ta tìm được hảm

thỏa mãn các điều kiện trên thì ta có một thuật toán xấp xỉ với tỉ lệ
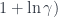
.
Bài tập:
Bài tập 1: Chứng minh Định lý 1.
Bài tập 2: Chứng minh Bổ đề 1.
Bài tập 3: Trong chứng minh Bổ đề 2, tại bước gần cuối, ta dựa theo Bổ đề 1. Tại sao ta cần

là monotone increasing. Nếu

chỉ là submodular function thì chuyện gì xảy ra?
Bài tập 4: Chứng minh Định lý 3.
Bài tập 5: Nếu

không là hàm số nguyên, thì Định lý 4 sẽ thay đổi như thế nào?
Nguồn: https://thaitramy.wordpress.com/2010/01/11/submodular-function/










